2585. Profit

The cows have opened a new business, and Farmer John wants to see how well they are doing. The business operates for n (1 ≤ n ≤ 10⁵) days, and on each i-th day, the cows record their net profit P_i (-1000 ≤ P_i ≤ 1000).

Farmer John wants to find the maximum profit that the cows have obtained during any consecutive period of time (note that a consecutive period of time can have a length from one day to n days). Help him by writing a program to find the maximum continuous profit.

Input. The first line contains an integer n. Each of the next n lines contains one integer P_i.

Output. Print the value of the maximum profit obtained during any consecutive period of time.

Sample input	Sample output
7 -3 4 9 -2 -5 8 -3	14

SOLUTION

sequence processing

Algorithm analysis

In this problem you should find a subsequence of consecutive numbers that will have the maximum possible sum among all such subsequences. If the maximum sum is achieved on the subsequence x_i, x_i+1, ..., x_j, then for any k, 1 £ k < i and l, j < l £ n, the sum of elements x_k, ..., x_i-1 and x_j+1, ..., x_l will be negative.

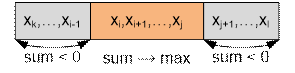
Kadane’s algorithm. Move through the array from left to right and accumulate the current partial sum in the variable s. If at any moment s becomes negative, we set s = 0. The maximum of all values of the variable s during the traversal of the array will be the answer to the problem.

Example

For the input sequence the maximum profit is 14.

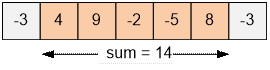
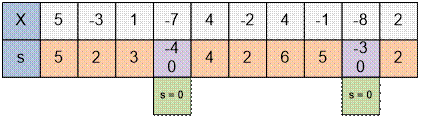
Consider an example of sequence X. Construct the partial sums. Reset the current value of the partial sum to zero when the sum becomes less than zero, and start counting the sum from the next number. The maximum value among all partial sums is 6, which is the answer. The desired subsequence will be 4, -2, 4.

Algorithm realization

Read the length of the sequence n. Initialize the value of the maximum profit max and the current partial sum s to zero.

scanf("%d",&n);

s = 0; max = 0;

Read n integers. Each read integer Number is added to the current sum s and we recompute the current value of profit max. If at any step the value of s becomes negative, set it to zero and continue the process.

for(i = 0; i < n; i++)

{

scanf("%d",&Number);

s += Number;

if (s > max) max = s;

if (s < 0) s = 0;

}

Print the answer.

printf("%d\n",max);

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int s = 0, max = 0;

for (int i = 0; i < n; i++)

{

int val = con.nextInt();

s += val;

if (s > max) max = s;

if (s < 0) s = 0;

}

System.out.println(max);

con.close();

}

}

Python realization

Read the length of the sequence n. Initialize the value of the maximum profit max_profit and the current partial sum s to zero.

n = int(input())

s = 0

max_profit = 0

Read n integers. Each read integer Number is added to the current sum s and we recompute the current value of profit max_profit. If at any step the value of s becomes negative, set it to zero and continue the process.

for i in range(n):

Number = int(input())

s += Number

if s > max_profit: max_profit = s

if s < 0: s = 0

Print the answer.

print(max_profit)